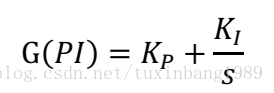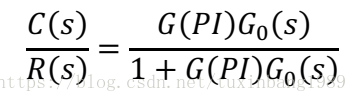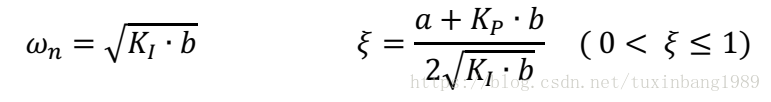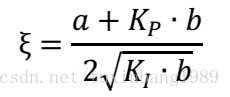实际控制系统主要的特点有:
①输入参考信号一般是阶跃信号、斜坡上升信号、时变信号,这些信号傅里叶分解后主要成分为直流和低频分量(几百赫兹以内);
②实际控制系统往往会存在干扰,包括信号采样的干扰、电压或电流的波动等,而这些干扰主要表现形式是中高频噪声(一般在500Hz以上)。
③控制对象的非线性,实际控制的仪器设备其物理量关系并非完全的线性关系,总是会存在一些时变、饱和、摩擦等非线性因素。
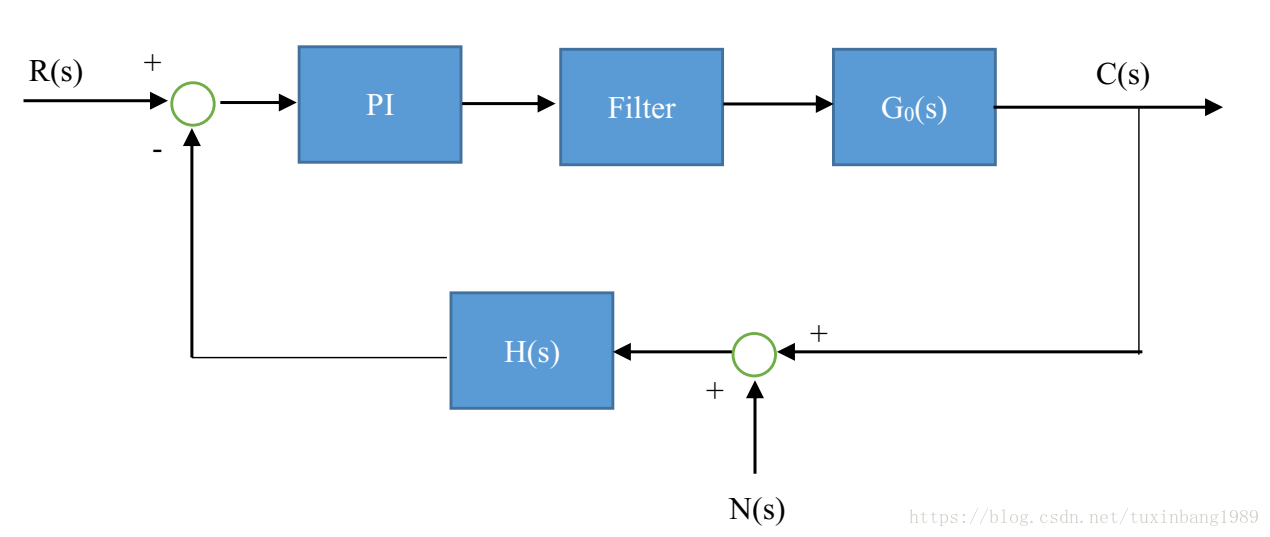
1.不加低通滤波环节的控制系统框图
G0(s)为被控对象的数学模型——传递函数,对于实际物体来说,如电能转换设备(电力电子)、电磁转换设备(电机)、电热转换设备(加热器)等,其代表的G0(s)一般为比例环节、一阶环节或者二阶环节,形如:
这些参数都是大于或等于0的数。
PI为比例-积分校正环节,用于对低频或直流信号控制的补偿,以使控制系统满足快速性、稳定性、准确性的要求。
H(s)是反馈传递函数,实际系统中通常是1。
R(s)为给定输入,对于一般控制系统来说,主要成分是直流或低频分量。N(s)是干扰噪声,通常为中高频小噪声。C(s)是输出量,对于线性系统来说,是R(s)和N(s)共同作用下的结果。这里要注意理解,传递函数或系统函数的s域或z域表达式代表的是控制系统对信号的计算过程,并不是对应什么时域信号表达式。这和输入输出信号、中间信号的频域表达式本质意义不同。
下面分别对R(s)和N(s)进行分析。
⑴若只有R(s)信号作用控制系统处理的是低频信号,令H(s)=1,系统闭环传递函数
特征方程为
由于系数均为正数,所以得到的特征根为负数根或实部为负数的共轭复根。
显然,有这一种趋势:Kp相对较大,KI相对较小时,特征根更倾向于负数根,响应C(t)的振荡不明显甚至没有;当Kp相对较小时,KI相对较大,特征根更倾向于共轭复根,这时响应会出现衰减的正弦振荡。当Kp过大时,有一特征根越接近0,则对应自由模态分量衰减慢,系统响应会出现较长时间的波动。
事实上,由于实际被控对象的非线性特性,C(t)一直在进行微小的变化和调整,呈现出微小的波动波形。
⑵若只有高频干扰信号N(s)作用时
令H(s) = l,
等效变换
后级闭环负反馈传递函数
第二项为一个二阶振荡环节。
对二阶振荡环节,设自然角频率和阻尼比
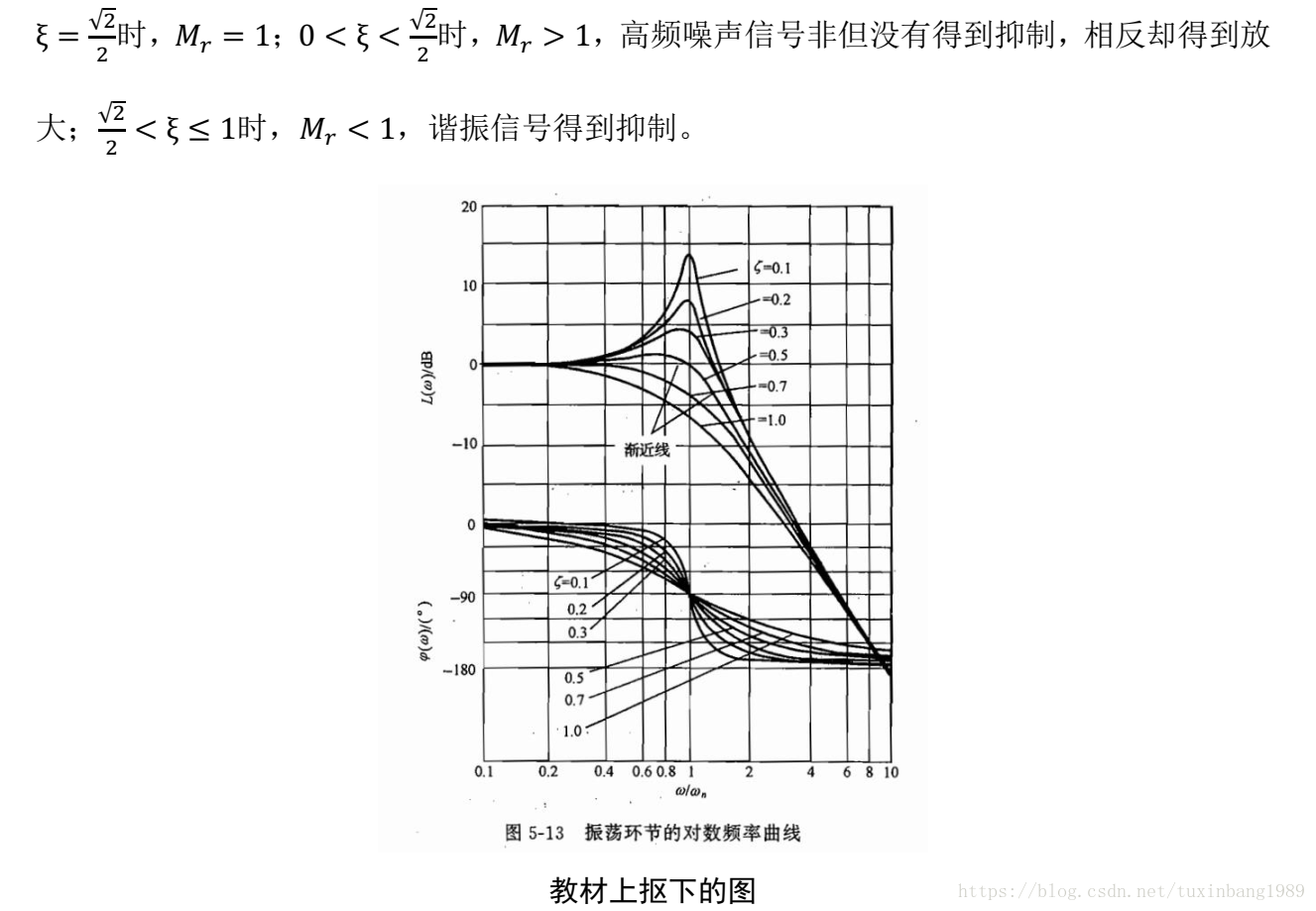
我们知道干扰N(s)是非常复杂的噪声,若其中包含较大量的频率在
附近的噪声,则会出现谐振峰,系统不但不能消除高频干扰噪声,还会放大噪声,造成输出物理量的剧烈波动。
影响谐振频率和谐振峰的参数(自然角频率和阻尼比),不仅有控制系统可以调节的参数KP和KI,还有被控对象本身物理特性固有的参数a和b。我们调节KP和KI参数,改变了系统的自然角频率和阻尼比,也就改变了谐振频率和谐振峰。根据以上分析,我们知道实际系统应增大其阻尼比
调节PI环节的参数时,应注意KP应大些,KI应小些。
2.低通滤波器的作用
低通滤波器可以滤除这些高频谐振及其附近的噪声,而对有用的低频信号可以基本无衰减通过,所以对于一个实际的控制系统而言,在控制系统中加入滤波器是必要的,否则可能会引起系统高频振荡。
还有一种情况,当自然角频率比较小时,谐振频率比较小,甚至比较接近有用信号的频率。这时若进一步减小低通滤波器的截止频率,则会对正常信号产生一定的衰减作用,不可取,这时可采用带陷滤波器滤除谐振频率,并能尽量减少对正常信号的衰减。
为什么系统会产生谐振?如何得到控制系统的谐振频率?
系统之所以产生谐振,是因为整个系统中含有极性相反的储能元件,即同时存在电感和电容性质的元件或控制环节。例如,电机绕组通电,但同时电机绕组也是一个电感;电流型并网逆变器通过中间大电感给电网放电。这些能量变换器件本身具有电感性质,而在反馈回路中含有RC硬件滤波或者数字低通滤波、积分环节等,这些有属于电容性质的组成部分。我们可以把整个系统看成一个既含有L,又含有C的电路。根据电路上的谐振知识,可知对一定频率的正弦信号,感抗和容抗会相互抵消,从而电路相当于只存在电阻性负载,也即发生了谐振。很明显,谐振的峰值根电阻性负载直接相关,电阻性负载越大,谐振峰越小。电路上用一个称为品质因数Q的参数来表示谐振的好坏—— Q=R*wC或R/wL。当品质因数越大时,谐振峰越小,谐振频带越窄,相当于电路品质越高一样;品质因数Q越小时,谐振峰越大,谐振频带越宽,好比电路品质越差。
根据设计的参数和被控对象的数学模型,搭建控制系统的simulink系统模型框图,或者编写对应的m脚本文件;之后导入到Matlab的LTI浏览器中,并查看系统的Bode图;根据bode图,可以直观得到控制系统的谐振峰所在频率。
事实上,低通滤波器并不能消除电路谐振,而是会使谐振点左移,即谐振频率变小;但是它可以消除因噪声干扰而带来的高频谐振。若是不加低通滤波器,传感电路所引入的高频噪声可能会在整个控制系统上产生谐振。
实际控制系统,更多的是高阶控制系统,一般可以找到主导极点,用二阶系统近似估算。这也是研究二阶系统的意义。 以上分析为经典控制理论,对于线性定常控制系统来说,具有一定的理论指导意义。实际用到的线性定常控制系统有温度控制器、液位控制器、电机驱动器、逆变器、开关电源、数控机床等。 另注:对于文中涉及到的低通滤波器和PI补偿器,可以参考本人相关的博客文章。